The domino portrait problem
In 1981 Kenneth Knowlton filed for a United States Patent entitled “Representation of Designs” [1] in which he proposed the use of dominos to render monochrome images. Twenty five years later, at the 2006 Conference on Constraint Programming, Artificial Intelligence and Operations Research (CP-AI-OR 2006), Robert Bosch gave an invited talk on “OptArt”, focusing on how optimisation could be used to create pictures, portraits, and other works of art [3,2]. In this talk, Bosch not only demonstrates the beauty of computer-generated art, but also the technical challenges involved in producing it.
A domino portrait is simply a rendering of an image based on a given number of sets of dominos. A set contains 55 dominos (double-nine dominos) and the dominos have to be used exactly once which makes the problem difficult. An efficient way to tackle the problem relies on a minimum cost flow formulation [4]. Thanks to the hard work of two students of UCC (John Horan, Eoin O'Mahony), the application to produce your own portrait is available on this page.
How is the problem stated ?
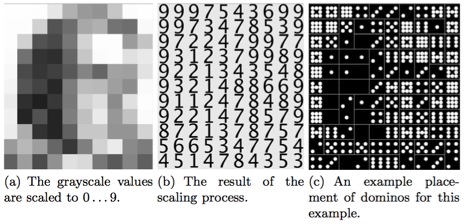
A domino portrait can be generated for any target image. The first step in the process is to convert the target image into a grayscale graphic image using, for example, the UNIX pgm command. Each pixel in a grayscale image is given a grayscale value between 0 (black) and 255 (white). The image is then divided in a grid with 2 * k * 55 cells where k is the number of sets used. Each domino has to cover exactly two adjacent cells of this grid. The mean gray value of all the pixels contained in each cell is computed and rescaled between 0 and 9 to match the number of dots of our dominos. Now when a domino is placed on a pair of cells, the error (or cost) is computed as the square of the difference between the value contained in the grid and the number of dots on the half-domino covering this cell.
The goal is to find a placement of all the dominos on this grid such that the overall error (the sum of the error of all cells) is minimum.
George Boole (1815-1864)
You can see here 5 portraits of George Boole made using 1,4,9,16 and 25 sets of dominos






Homer
A portrait of Homer made of 25 sets of dominos

Mimitte
A portrait of Hadrien's cat with 49 sets of dominos !

Sofware
The following application allow you to create your own domino portraits. You can download it as jar archive and run it on your computer by double-clicking on the jar. You can also try the applet domino appet.
It is very easy to use :
First, select the picture and use the floating frame to capture the area you want to convert in dominos. This application is made for portraits and work better if you focus on the face and don't leave too much background. Moreover, the quality of the rendering also depends on the amount of balck and white in the picture once converted in a gray format. If the white and black are well balanced,it is definitely better. Notice that the inside frame can resize itself because the size has to fit the number of dominos (second step).
Second, select the number of sets of dominos. You can put a very high number of sets and the more you have the better is the approximation (this number is constrained to be a perfect square). However, the magic appears when you can really see the dominos in the resulting image. So the goal is to find the minimum number of dominos that gives a good approximation of your picture.
Third, select the solving technique. Three choices are available but the two last one are the more efficient ones. The last called "MCF & Local Search" applies first the second one called "Minimum Cost Flow" and try to improve further the picture. We recommend the last one that usually require at most one minute.
Finally, after pressing "start", the first solution found by MCF is shown and a red signs "processing" appears during the local search phase. Wait for this sign to diseappear to save the picture !
References
[1] Kenneth C. Knowlton. Representation of designs. U.S. Patent # 4,398,890 (August 16th, 1983).
[2] E. Berlekamp and T. Rogers. The mathemagician and pied puzzler: A collection in tribute to martin gardner. AK Peters, 1999.
[3] R. Bosch. Constructing domino portraits. Tribute to a Mathemagician, pages 251–256, 2004.
[4] Hadrien Cambazard, John Horan, Eoin O'Mahony, and Barry O'Sullivan. Fast and Scalable Domino Portrait Generation. Proceedings of CP-AI-OR 2008. [.pdf][french.pdf][talk.pdf]
Links
http://www.maa.org/mathland/mathtrek_04_14_03.html
http://www.dominoartwork.com/
http://4c.ucc.ie/~eomahony/Site/Welcome.html