The Kakuro Problem
The puzzle is to fill a grid with numbers between 1 and 9 such that :
- The sum of a continuous block of white cell in horizontal (or vertical) direction must be equal to the hint given in the black cell to the left (above).
- All numbers in a continuous block of cells must be pairwise different.
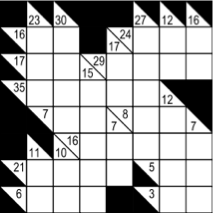
The two following pictures show an instance and a solution :

A Constraint Programming Model
A natural way to model the puzzle in Constraint Programming is to associate a variable, x_i, per cell of the grid with a domain [1,9]. Then each sequence S_j of contiguous cells has to be alldifferent and its sum is also constrained by the corresponding hint, h_j.
The constraint model turns out to be very simple :
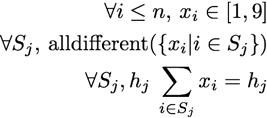
Its main weakness is to express the sum and alldifferent as a conjunction of two different constraints therefore losing critical reasoning for the puzzle.
Let illustrate the propagation performed by sum and alldifferent and show what is missing :
Imagine a sequence of four variables which have to take different values with their sum equal to 11 and the following domains :
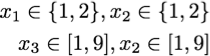
Let's have a look at the reasoning achieved by the solver.
The sum usually performs bound propagation and compute a lower and upper bound of the sum to 4 (1+1+1+1) and 22 (2+2+9+9) respectively.
The alldifferent is however able to remove values 1,2 from x_3 and x_4 (a set of two variables having the two same possible values imply that the corresponding values have to be removed from all other domains) resulting in :
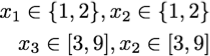
The sum is therefore able to update the previous bounds to 8 and 22 which are still consistent with the required 11 and a fix point is reached here.
We can only go further by combining reasonings on the sum AND alldifferent and see for example that the upper bound of any variable can not be greater than 5, indeed,
5 + (1 + 2 + 3) = 11. 1 + 2 + 3 being the minimum quantity we can have for three alldifferent variables, the remaining one can thus not be greater than 5 or we would have a contradiction with the fact that the sum has to be equal to 11. It can also be seen that 4 is impossible for x_3 and x_4 and the resulting generalized arc-consistent domains would be :
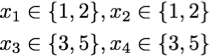
How do we encode that in the constraint model to help him mimic human reasoning and achieve a stronger level of consistency ?
We could develop a dedicated sumAllDiff constraint but it is far beyond this tutorial :) so let's use generic arc consistency algorithms available in the solver.
Notice that all reasonings involved here are quite simple, the difficulty is often more about finding an efficient algorithm to perform them (think at the reasoning described here for the alldifferent for example, does it involve checking all subsets of variables ? that wouldn't be polynomial...).
Strengthening Propagation
The idea suggested in [1] is to use the regular global constraint [2] by compiling the possible solutions of a sumAlldifferent constraint and performing arc-consistency on the resulting automaton. However, this can represent a lot of tuples (in the worst case, 9 variables of domain [1,9], that's 9! tuples). So our solver will proceed incrementally by propagating constraint after constraint to simplify the problem as much as possible before creating the corresponding regular contraint when needed for unknown variables.
The source code available further based on the choco solver [3] proceeds as follow :
1- compute accurate bounds for each kind of sumAllDiff (identified by the length of the sequence and value of the sum)
2- then create the choco variables for the cells with accurate bounds computed previously for each sumAllDiff sub problems
3- post the sumAllDiff as the conjonction of sum and alldiff and propagate them to start simplifying the problem
4- sort the sequences from the smallest to largest, post the sumAllDiff represented this time as a regular and propagate it immediatly to simplify the problem at each step and speed up the generation of the next regular.
5- apply a step of shaving if all the cells are not known at this stage. Shaving is a technique that check if the network of constraints can be made arc-consistent for each value of each variable. If not, the value is therefore removed. It can be seen a stronger form of consistency (singleton arc consistency).
6- call a solve if there still exists a non intantiated cell in the grid. (this is very unlikely to occur and puzzles are solved by the previous reasonings only in practice)
The result is that most of the puzzles are solved before step 5, without any search.
Resources
The choco sources implementing the solver described previously are available here [.zip] (java 1.6 is needed). A jar file of the kakuro solver can also be dowloaded [kakuro.jar] and work with [choco-1_2_06.jar].
Three data sets generated by Helmut Simonis can be used as benchmark :
- Easy puzzles [.ecl]
- Medium puzzles [.ecl]
- Difficult puzzles [.ecl]
For some reasons, the files are in the format of Prolog facts. A parser is included in the application which can be called the following way :
java -jar kakuro.jar data_generated_easy.ecl
Notice that the jar of choco, choco-1_2_06.jar has to be in the same directory.
It outputs the solution of each puzzle and show some statistics of the resolution of all the puzzles such as average and max time as well as the percentage
of puzzles solved without shaving.
Thanks to John Horan for his help to make this quickly available.
References
[1] H. Simonis. Kakuro as a Constraint Problem. Unpublished, 2007 (http://4c.ucc.ie/~hsimonis/kakuro.pdf)
[2] Gilles Pesant, A Regular Language Membership Constraint for Finite Sequences of Variables, CP 2004. Pages 482-495, LNCS 3258, Springer-Verlag, 2004.
[3] the choco solver : http://www.emn.fr/z-info/choco-solver/